I recently looked at the date when I wrote the last Coffee Chat and was astounded at how much time had gone by. How time flies when you are having fun (in quarantine). So, with apologies, I would like to return to the subject of the last Chat, which was entitled “Secret Sauce.” If you want to review that, you can read it here on the Midsummer’s Music website, but here is the gist of it.
We know that the three main ingredients in music are melody, rhythm, and harmony. I believe that the first two are fairly easy to grasp. Harmony is more elusive, especially if you didn’t grow up playing the piano (or guitar) – hence, the Secret Sauce. But as I pointed out in our last Chat, we all understand quite a bit about harmony intuitively. Why? Here we confront some controversy. Some maintain that there is a physical reason that certain harmonies are just that – harmonious. Others, especially many “experts,” say it is a learned pattern. I think it is some of both, but I really think that there is a basis in physics that should not be overlooked. In fact, our ancestors, going way back, really thought that harmony controlled much of our environment, especially the heavens. They termed it the “Harmony of the Spheres.” There were some real knock-down, drag-out fights about this over the centuries from the Greeks until at least the 18th century.
This all centered around a discovery by Pythagoras five centuries B.C., asserting that when you hear a pitch, you are not hearing just one pitch, but a composite of many pitches. We now know that Pythagoras was spot on. In fact, if we were together in a room with a piano, I could demonstrate what he was getting at very easily. Since we are socially distancing, gather ‘round my imaginary piano and listen to this. I am going to strike a C in the lower register of the piano, but before I do, I am going to very, very gently depress the C key an octave above, so gently that no sound is made, but in doing so, I have taken the damper off the strings for the upper C. Now, with that upper C unfettered by a damper, I am going to strike the lower C forcefully and then release the lower C key very quickly. As a consequence, the lower C, which I struck loudly, is now cut off abruptly and has stopped sounding because by releasing the key, its damper has now stopped the sound. Pianos must have these dampers, otherwise you couldn’t control the length of any note. The strings would keep sounding until they eventually completely evaporated into thin air.
So, having struck my lower C and let it go, it sounded and abruptly stopped. But because I have the C key an octave above silently depressed and its strings free to vibrate, I can now hear, not the lower C string, but the higher one that is undampened. That is because the upper string is free to vibrate sympathetically.
At this point, it is important to remember that any note or pitch is caused by something vibrating – your vocal cords (just put your fingers on your voice box and say the word MUSIC), an oboe reed, the lips of a trumpeter, the strings on a violin, etc. Each pitch has its own discrete number of vibrations. You may have heard that the orchestra tunes to A 440. That is the A above middle C, and whatever is vibrating to make the sound is doing so 440 times/second. Only that A, in that particular octave, has that number of vibrations/second. So, let’s say the C below middle C, which we thumped loudly on the piano, has a pitch of 130 vibrations/second (this number is an approximation for simplicity). We heard that note sound for a split second upon being struck, but now we are hearing the C above because that string is free to vibrate since I am still depressing the key. This happens to be Middle C, and it is vibrating at 260. What you will quickly notice is that it is twice the number of vibrations of the lower C. So, the note an octave above happens to be vibrating at a ratio of 2/1. This is true for all octaves. It also happens to be the first overtone of the note we originally struck. Pythagoras discovered that this overtone existed for virtually every basic or fundamental pitch that is sounded. He didn’t have a piano to work with of course, but we just demonstrated that Pythagoras was correct. Since we didn’t actually “sound” our upper C, it had to be activated by something in the lower note, and that something was the first overtone of the lower C. Since that octave overtone is present in the lower note (and has a frequency therefore of 260) it sets in motion our freed-up string(s) of the C above (that also has a frequency of 260). That’s the nature of sympathetic vibration. You have to have two elements that can vibrate, which share the same (or very close to it) natural frequency and therefore excite one another.
This means that our lower piano string is not only vibrating at 130, but simultaneously is vibrating at 260 (that’s what’s activating the upper string). That’s a very talented string, right? In order to do this, it is not only vibrating at its full length, but it is also dividing itself in two and each of those halves are vibrating in order to give us the 260 number. David Perry could demonstrate this on his violin by playing his open G string to sound the lowest note on the violin, and then put his finger down on that same string halfway up to the bridge at which time it would play an octave higher. But even when he is playing the open string with no fingers, that upper octave (overtone) is still there as part of the lower note, just at reduced volume. That overtone is part of the profile of the basic note and helps give it character or depth. We don’t hear it distinctively because it blends in so well.
However, and here is where it gets really fun, there are more overtones – many more, and Pythagoras was on the job back there in sunny Greece and found them. The next overtone above the octave we just identified is a 5th above the C, which is a G (count up five white notes from C and you come to G – hence it’s called a 5th). So, if I’m telling the truth, I can go back to the piano and depress that G key ever so quietly to just release the damper without making a sound, I can thump the low C again and release it, and voila!, we hear a kind of ghostly G coming out of the piano at the same pitch as the depressed key would sound if actually struck. We now know that we have our low C, which is enhanced by the C an octave above it, and a G a 5th above that (that would be the G above middle C). That G happens to be vibrating at 390 vibrations per second. That got Pythagoras pretty excited because the ratio of the C at 260 to the G at 390 is 260/390 or simply 2/3.
Guess what. The next overtone is a C above that G we just discovered, or the one two octaves above the original C. More excitement. It vibrates at 520, which is 4 times the lowest C and twice that of the C in between. Not only that, but the distance between the G at 390 and this new C at 520 is the ratio of 3/4. It is the interval of a fourth. So now, hidden in what seems like a humble lower C on the piano, we have the most basic intervals for virtually every kind of music in the world, the octave, the fifth, and the fourth. And again, our note is generating all of these overtones simultaneously and is therefore vibrating not only as a whole string (in the case of a piano or violin), but also is concurrently dividing itself in two (to get the octave), into 3 (to get the 5th) into four (to get the 4th), etc. As I say, very talented string!
We can keep going with this exercise to see that the next overtone is an E (a major 3rd) above the last C, and the next after that is another G, which gives us a minor 3rd. We now have the basic intervals that are used in our most primary chords in western music. Although I would like to demonstrate this to you myself in person, given the circumstances, I am going to turn to my friend William Magalio who has created a YouTube presentation, much like I would do if we were together in person.
Actually, I have never met Mr. Magalio, but I would like to thank him for doing this. So, having experienced this demo, you can see why I might not entirely agree with the “experts” who think that our western system of scales and chords is entirely a learned accident. We may attune ourselves to it, but it is partly because it is all around us in nature. From birth (and even prenatally) we are immersed in a recipe or cocktail of sound combinations that is preordained. Virtually every tone we hear consists of not just the basic note, but this whole composite of overtone notes as well. Despite the fact that the overtones can be isolated using a method like Mr. Magalio did, we don’t normally hear notes this way. We hear the whole package as one note, perhaps a C (as in this case, or an F, with its own group of overtones, etc.). To use another food analogy (which I seem wont to do), it is similar to the way we might taste a Mexican mole sauce. We don’t taste the nearly 20 ingredients separately. We just say, “MMMM, delicious sauce.”
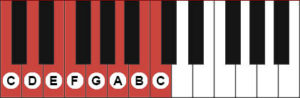
However, let’s see what secret we can extract from our overtone ‘mole sauce.’ In the keyboard representation below, each note of the scale has a number. So, C is 1, D is 2 (or a 2nd above C), E is 3 (or a 3rd above C), etc.
C Major Scale
Therefore, the C major chord (below) is made up of a major 3rd (C to E), and a minor 3rd (E to G). It is a minor 3rd because it has one less half-step in it than the major third. Another way of distinguishing between the two types of thirds in the C major chord is the major 3rd (C – E) has one white key and two black keys, whereas the minor third (E – G) has one white key and only one black key. The distance between the bottom note (C) and the top (G), is a 5th. This can be replicated in whole or in part in the next octave above or in any octave. So, if we included the next C above our basic chord, we would have the interval of a 4th between the G and the top C.
C Major Chord
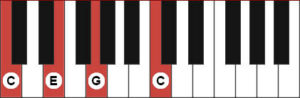
So, now you know how to ‘spell’ (to use music theory lingo) a C major chord. But that’s not the main point. The point is to see why this chord is important to us and why we have a fondness for it. Let’s go back to our overtone series:
The bottom (or fundamental) note is the one Mr. Magalio thumped on his piano to make the overtones. The first C (in black) is the first overtone that he separated out for us. Then he added the 5th to it. Now, notice that the 3rd, 4th, and 5th overtones (C – E – G) are exactly the same red notes that you saw on the keyboard above. This should clearly demonstrate that the C major chord isn’t just something that some choral composer in the 15th century decided sounded good to him. It is something that exists all around us and has ever since the world began. We are immersed in it every day whenever we hear a tone, and have been since we were in the womb. It is our primordial harmonic soup. Is it surprising that the major chord has a familiar ring to it? It is only that it took until around the 15th century, perhaps for some choral church composers, to begin to see the possibilities lurking there before their very ears.
If you look again at the example just above with the fundamental and the first 5 overtones, and you think about all those pitches being sounded simultaneously, you realize we are talking about what is called harmony – the simultaneous sounding of different pitches. This particular combination of pitches is preordained, but it wasn’t until our imaginary choral church composers started thinking about this harmonic or vertical way of combining notes that vast harmonic possibilities started to open up for music. Prior to this, the fundamental way of thinking was horizontal or melodic. Now the game was starting to change, ever so slowly at first, as the harmonic (vertical) dimension was added into the mix.
Next time we will look at the implications of this new way of thinking. It was the chance combination of tin and copper that led to the Bronze Age. It was as if we had just invented the wheel. How long ago was that yet how recent the development of the Segway. We are still figuring out the harmonic possibilities those choral composers unleashed 5 centuries ago. We’ll go into that a bit more next time. Meanwhile, go find a piano and see if you can unleash some overtones. Once you’ve figured it out, it is a great party trick.